W roku szkolnym 2019/2020 badaliśmy problem filtra mydlanego, zastanawiając się czy takie urządzenie może służyć do oddzielania małych i lekkich cząsteczek od dużych i ciężkich. Zagadnienie to było przedmiotem zawodów Turnieju Młodych Fizyków 2020, który niestety w związku z panującą pandemią się nie odbył. Poniżej znajduje się krótkie podsumowanie wyników naszej pracy. W celu wyznaczenia zdolności membrany do filtrowania cząstek wprowadziliśmy model teoretyczny oparty o zasady zachowania energii w układzie. Przeprowadzając odpowiednie doświadczenia zbadaliśmy wpływ takich czynników jak promień zrzucanej kulki oraz promień membrany.
Filtr mydlany zachowuje się odwrotnie niż zwyczajne sitko. Zwykłe sito przepuszcza małe drobinki, a zatrzymuje większe obiekty. W przypadku filtru mydlanego duże obiekty (w stosunku do wielkości membrany) zostają przepuszczone, natomiast mniejsze pozostają na membranie (co można zobaczyć na poniższych filmach). Ta właściwość błony mydlanej znajduje zastosowanie w medycynie. Taki filtr uniemożliwia przedostawanie się niepożądanych gazów lub innych drobin z powietrza na miejsce rozcięcia. Jednocześnie błona przepuszcza narzędzia chirurgiczne, a poprzez dodanie odpowiednich substancji do roztworu błony mydlanej, od razu je dezynfekuje [1].
Opis jakościowy
Błonę mydlaną można utworzyć dzięki dodaniu do wody niewielkiej ilości surfraktantu (detergentu). Nie jest jednak oczywiste w jaki sposób surfraktant wpływa na powstanie błony i dlaczego jego dodanie pozwala otrzymać bańki mydlane o czasem bardzo dużych rozmiarach (o objętości nawet 96.27 m). Popularnym, lecz błędnym, wyjaśnieniem jest stwierdzenie, że bańki mydlane powstają gdyż surfraktant zmniejsza napięcie powierzchniowe wody. Jest to dalekie od prawdy, gdyby tak było, to można by było otrzymać bańki mydlane (lub alkoholowe) używając spirytusu, który ma około 3 krotnie mniejsze napięcie powierzchniowe niż woda. Wpływ surfraktantu na powstawanie baniek jest bardziej subtelny.
Cząsteczki surfraktantu dodanego do wody lubią się ustawiać na granicy woda-powietrze w taki sposób, że część hydrofobowa (o słabym powinowactwie do wody) surfraktant znajduje się bliżej powierza, a część hydrofilna (o silnym powinowactwie do wody) bliżej wody. Błona mydlana powstaje poprzez zamknięcie bardzo cienkiej warstwy wody pomiędzy dwiema dwiema granicami woda-powietrze. Taka konfiguracja jest bardzo stabilna, co zawdzięcza efektowi Marangoniego. Gdy w błonie mydlanej powstanie zaburzenie, które mogłoby prowadzić do przedziurawienia się błony, następuje zmiana koncentracji cząsteczek surfraktant na powierzchni woda-powietrze, co prowadzi do zwiększenia napięcia powierzchniowego w okolicach miejsca gdzie bańka jest najcieńsza. Taka konfiguracja jest niekorzystna energetycznie, a ponieważ układy fizyczne dążą to takich ustawień, gdzie energia potencjalna układu jest minimalna, można powiedzieć, że błona mydlana "nie lubi" zaburzeń grubości. Takie zachowanie błony uniemożliwia powstanie fluktuacji powierzchni powodujących zetknięcie się granic woda-powietrza po obu stronach błony i tym samym powstania dziury w błonie.
W przypadku rozważanego filtra mydlanego, kiedy kulka dotyka błony mydlanej staje się ona krańcem granicy faz pomiędzy wodą a powietrzem – w takiej sytuacji działa na nią bezpośrednio siła napięcia powierzchniowego. Ta siła jest proporcjonalna do długości linii, na której stykają się woda, powietrze i kulka; jest skierowana zgodnie ze styczną do powierzchni woda-powietrze. Kulka opadając przez błonę działa przeciw sile napięcia powierzchniowego wykonując pracę, a zatem zmniejsza swoją energię kinetyczną kosztem energii potencjalnej błony. Jeśli kulka "zużyje" całą energię potencjalną błony to nie uda się jej zatrzymać, w przeciwnym wypadku kulka pozostanie na powierzchni.
Ponieważ cięższe obiekty mają większą energię kinetyczną, niż lekkie obiekty (zrzucone z tej samej wysokości), można się spodziewać, że błona będzie miała większą szansę na zatrzymanie tych drugich. Podobnie można się spodziewać, że obiekty zrzucone z niższej wysokości zatrzymają się na błonie, a te które zostały zrzucone z wyższej wysokości przez nią przelecą.
Model Teoretyczny
W celu określenia co to znaczy duża masa, oraz duża wysokość potrzebny jest ilościowy opis zjawiska. Na potrzebę wprowadzenia matematycznego opisu filtra mydlanego założono, że błona mydlana ma jednorodną grubość oraz napięcie powierzchniowe, które nie zmienia się wraz z rozciągnięciem błony. Przyjęto, że siły napięcia powierzchniowego są dominującymi siłami działającymi na błonę, oraz że przelatująca przez nią kulka porusza się po torze będącym osią symetrii obręczy, na której jest rozpięta błona.
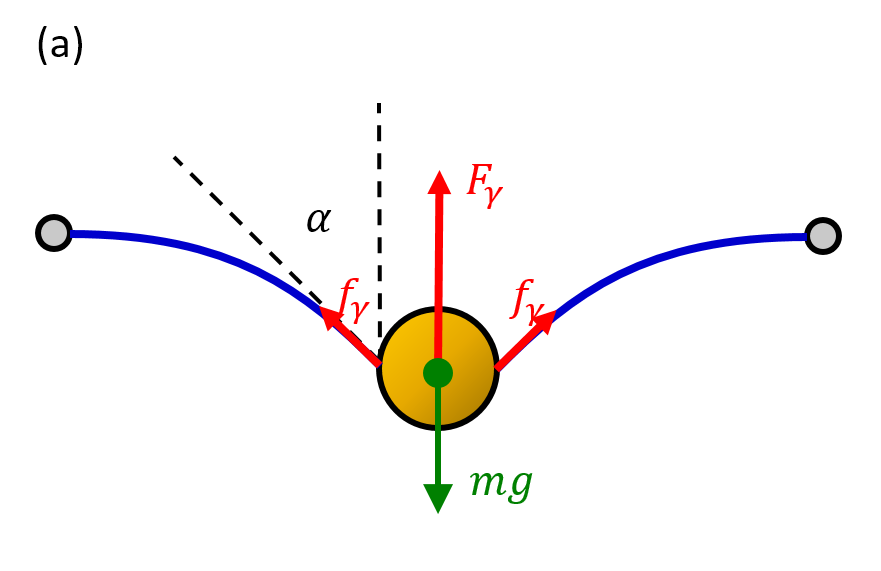
Gdy kulka przelatuje przez błonę, na jej powierzchni powstaje brzeg błony mydlanej. Na tym brzegu błona mydlana oddziałuje z kulką siłą napięcia powierzchniowego skierowanego w kierunku stycznym do powierzchni błony. Wypadkowa siły napięcia powierzchniowego jest równa obwodowi okręgu styczności błony z kulką pomnożonemu przez gęstość siły (napięcie powierzchniowe) oraz przez cosinus kąta jaki tworzy styczna do błony z osią symetrii:
Siła ta przeciwstawia się sile grawitacji. Porównują obie siły, można wyznaczyć górne ograniczenie na masę kulki. Analizując postać siły napięcia powierzchniowego można stwierdzić, że jej wartość jest największa gdy promień okręgu styczności jest równy promieniowi kulki, a styczna do błony na granicy z kulką jest skierowana pionowo do góry. W ten sposób otrzymuje się, że kulka która może być utrzymana przez błonę musi mieć masę mniejsza niż:
Nawet jeśli masa kulki jest nie duża, może one przelecieć przez błonę, gdy porusza się z wystarczająco duża prędkością. Znalezienie maksymalnej energii kinetycznej, z jaką może poruszać się kulka tak aby zostać zatrzymaną przez błonę, jest bardziej skomplikowanym wyzwaniem i wymaga określenia kształtu błony odkształconej przez przelatującą przez nią kulkę. W sytuacji statycznej, błona przyjmuje kształt, który minimalizuje jej energię potencjalną przy zadanych warunkach brzegowych. Jeśli jedynym źródłem energii potencjalnej jest energia napięcia powierzchniowego, błona przyjmie kształt, który minimalizuje jej powierzchnię. W przypadku błony rozpiętej na okrągłym pierścieniu błona o najmniejszym polu powierzchni jest kołem. Z kolei dla błony rozpiętej na dwóch pierścieniach, korzystając z rachunku wariacyjnego, można pokazać (o ile pierścienie nie są rozsunięte za daleko), że błona przyjmuje kształt katenoidy. W rozważanym modelu przyjęto, że błona w każdej chwili czasu osiąga stan równowagi statycznej (przybliżenie kwazistatyczne) i zawsze graniczy z kulką na jej równiku – tj. jest rozpięta między dwoma okręgami będącymi: pierścieniem o promieniu oraz równikiem kulki o promieniu
.
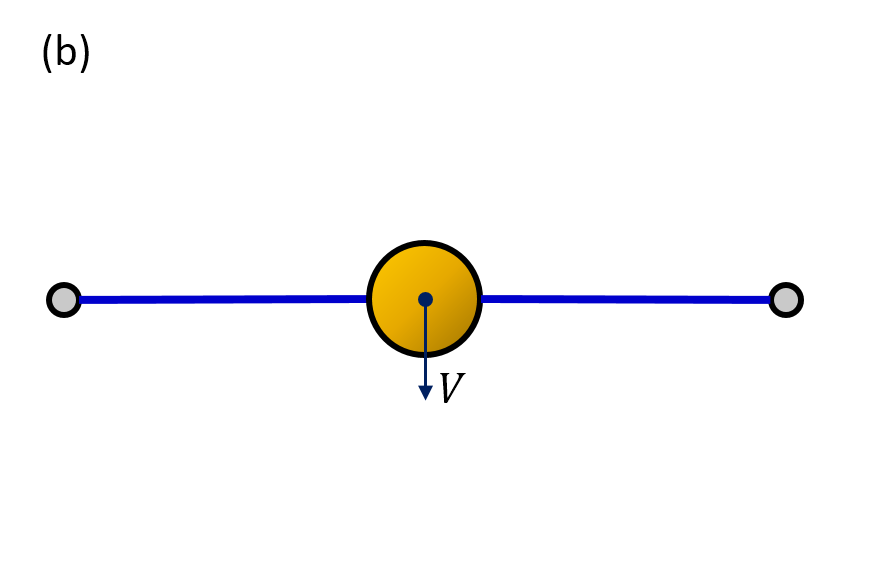
W celu oszacowania zmiany energii błony w trakcie, kiedy kulka przelatuje przez nią, porównano dwie chwile czasu: gdy kulka znajduje się na błonie i jeszcze nie spowodowała jej znacznego odkształcenia, oraz gdy styczna do błony w miejscu styku z kulką jest równoległa do osi symetrii (tj. błona działa na kulkę z maksymalną siłą). Energię powierzchniową błony w pierwszym przypadku można zapisać w postaci:
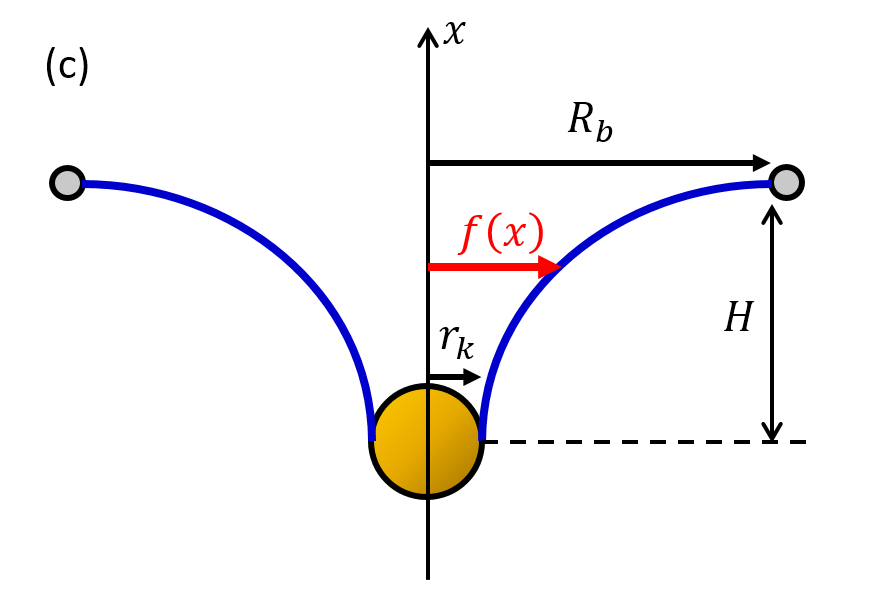
W drugim przypadku w celu wyznaczenia pola powierzchni błony, najpierw zostanie określona tworząca kształtu błony. W rozważanym przypadku tworząca jest katenoidą zadaną funkcją:
korzystając z tego wzoru można pokazać, że wychylenie błony jest równe:
Znając tworzącą, pole powierzchni bryły można określić korzystając ze wzoru:
co prowadzi do ostatecznego wyniku:
Porównując początkową energię potencjalną kulki oraz maksymalną różnicę energii potencjalnej błony, jaką może ona uzyskać w skutek odkształcenia przez kulkę, można określić maksymalną wysokość z jakiej zrzucona kulka może zostać zatrzymana przez błonę:
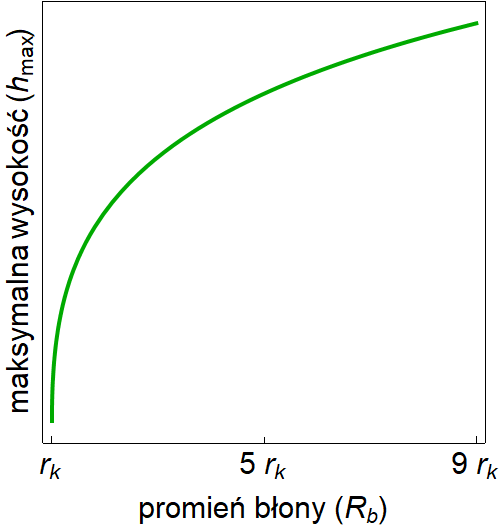
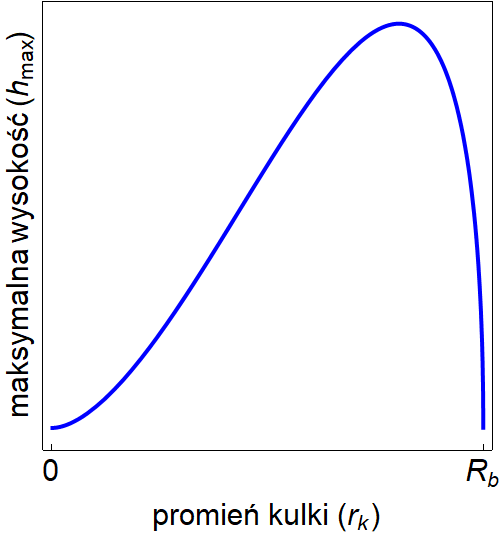
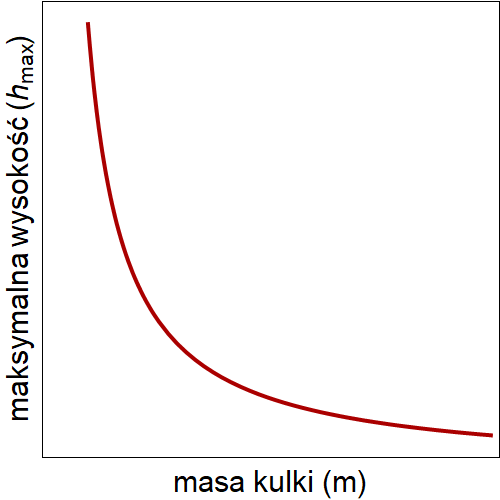
Jak widać z powyższej zależności, wysokość z której może zostać zrzucona kulka jest proporcjonalna do napięcie powierzchniowego oraz odwrotnie proporcjonalna do masy kulki. Przy ustalonej masie oraz napięciu powierzchniowym, zależność od promienia kulki oraz błony jest mniej oczywista. Wykreślając postać wyrażenia znajdującego się w kwadratowych nawiasach powyższej funkcji można pokazać, że maksymalna wysokość jest rosnącą funkcją promienia błony. Gdy promień kulki rośnie, początkowo również rośnie maksymalna wysokość, z której można zrzucić kulkę, funkcja ta osiąga ekstremum, powyżej którego tendencja jest odwrotna. Można pokazać, że maksymalna wartość h jest osiągana gdy stosunek promienia kulki do promienia błony jest równy około:
.
W powyższym wyprowadzeniu przyjęto szereg założeń i skorzystano z uproszczeń, które ułatwiły znalezienie prostych zależności określających maksymalną masę kulki oraz wysokość z jakiej może ona zostać zrzucona. Prawdziwość i zakres stosowalności otrzymanych wniosków została zweryfikowany doświadczalnie.
Układ doświadczalny
Płyn mydlany potrzebny do uformowania błony wykonano mieszając: 20 ml wody, około 10 ml detergentu oraz 6 ml gliceryny. Każdy z odczynników starannie odmierzono za pomocą strzykawki i tak przygotowany roztwór wylewano na szalkę Petriego. Dodanie gliceryny zwiększa lepkość mieszaniny, co spowalnia przepływ cieczy wewnątrz błony. Ponieważ na ciecz w błonie działa siła grawitacji, będzie ona przepływać do najniższego punktu błony i się tam gromadzić. Skutkując coraz to cieńszą warstwą błony w punktach położonych wyżej, co w końcu doprowadzi do przerwania błony. Zwiększenie lepkości cieczy pomaga przeciwstawiać się temu zjawisku i w rezultacie pomaga wydłużyć czas "życia" błony.
W celu charakteryzacji otrzymanego roztworu, wykonano pomiary jego napięcia powierzchniowego. W tym celu posłużono się metodą kropelkową przy pomocy układu składającego się z pipety, o średnicy główki () równej 3 mm, napełnione roztworem, umieszczonej pionowo nad wagą. Poprzez powolne ściskanie główki pipety wypuszczano z niej kolejne krople roztworu na znajdujące się poniżej naczynie. Zmierzono kilkukrotnie łączną masę kropli otrzymanych tym sposobem i wyznaczono średnią masę 1 kropli (
). Ponieważ tuż przed oderwaniem kropli siły ciężkości i siły napięcia powierzchniowego kropli się równoważą, korzystając ze wzoru:
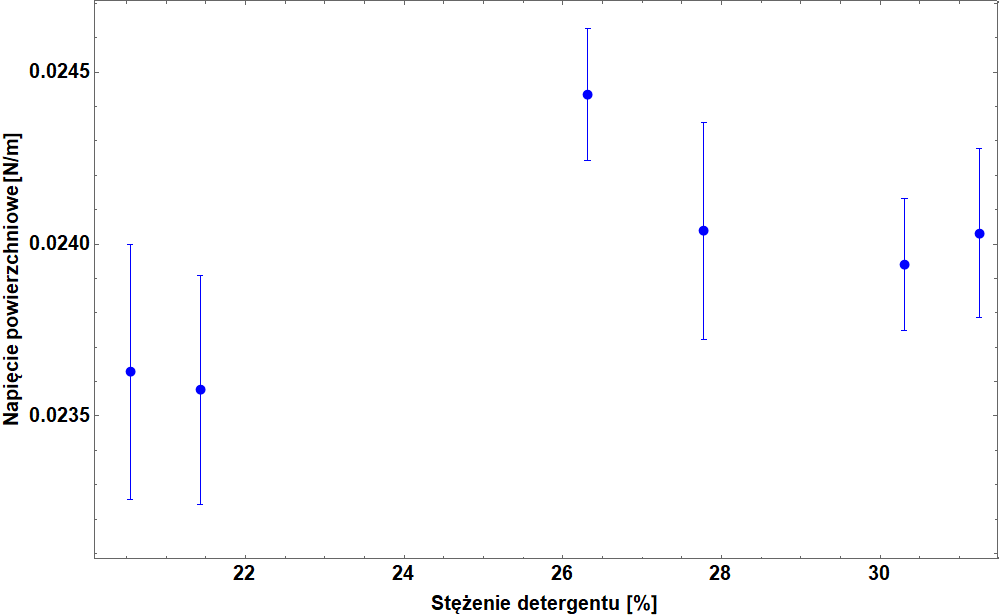
można oszacować wartość napięcia powierzchniowego (). Wyniki pomiarów przedstawiono na poniższym wykresie, dla badanego płynu mydlanego, dla którego stężenie detergentu wynosiło 30% napięcie powierzchniowe było równe: (23.9 ± 0.2) ✕ 10-3 N/m.

W celu przeprowadzenia badań filtra mydlanego wykonano dwa układy pomiarowe. Pierwszy z nich posłużył do wykonania jakościowych obserwacji zachowania błony. Drugi zastosowano do pomiaru parametrów wpływających na przepuszczalność błony. Obręcz użytą do pomiarów jakościowych zbudowano z drutu uformowanego w kształt koła o średnicy 3.5 cm. Z tego samego drutu zrobiono rączkę, za pomocą której membrana była sztywno zamocowana do łapy na statywie. Obok membrany umieszczono linijkę, która posłużyła do pomiaru odległości. Błona była formowana poprzez zanurzenie aluminiowej obręczy w płynie mydlanym, a następnie powolne jej podniesienie. Przez membranę zrzucano kulki o średnicy 1 cm, a zjawisko było rejestrowane przy pomocy kamery wideo w prędkości 200 klatek/s.

W układzie służącym do zbadania parametrów wpływających na przepuszczalność błony metalową obręcz zastąpiono puszką otwartą z jednej strony. Błonę mydlaną otrzymywano poprzez zanurzenie otwartego końca aluminiowej puszki w płynie mydlanym. Od spodu puszka miała wydrążoną dziurę, która służyła temu aby wyrównać potencjalną różnicę ciśnień (atmosferycznego i tego w środku puszki). Ponieważ otwór puszki jest prawie idealnie okrągły taka metoda wytworzenia błony mydlanej pozwalała na otrzymanie osiowo symetrycznej błony oraz powtarzalnych pomiarów. W doświadczeniach użyto puszek o średnicach: 2.7 cm, 4.4 cm, 5.6 cm, 6.3 cm i 7.8 cm.
Kulki były wykonane z utwardzonej modeliny ich średnicę zmierzono przy pomocy suwmiarki. Masę większych kulek (ich promień wynosił od 1.5 do 3.5 mm) zmierzono przy pomocy wagi (z dokładnością do mg). Masa najmniejszej kulki (o promieniu 0.75 mm) była mniejsza niż dokładność wagi, więc by ją obliczyć wyznaczono gęstość modeliny z której była zrobiona kulka. W tym celu zmierzono masę i objętość dużego kawałka modeliny. Szukaną gęstość obliczono korzystając ze wzoru:
gdzie przez V oznaczono objętość kulki. Otrzymana gęstość wynosiła ona 1581 kg/m3. Zakładając, że badana kulka jest idealną kulą i znając jej promień można obliczyć jej objętość. Podstawiając objętość i gęstość najmniejszej kulki do powyższego wzoru obliczono jej masę.
Nad puszką na znanej wysokości zamontowano patyczek z zaznaczonym miejscem, z którego zrzucano kulki. Kulki umieszczano za pomocą pęsety i delikatnie zsuwano z patyczka. Umożliwiało to dokonanie wielu pomiarów z kulkami spadającymi zawsze z tej samej wysokości i zerową prędkością początkową.
Pomiary
Pomiary zależności przepuszczalności błony w zależności od jej promienia wykonano dla pięciu różnych średnic błony poprzez zrzucanie na nie kulki o promieniu 1 mm i masie 5 mg. Sprawdzano czy dla danej wysokości zrzucania kulka przejdzie przez błonę czy pozostanie na jej powierzchni. Każdy z pomiarów powtórzono 20 razy. Uznano, że kulka pozostaje na powierzchni błony dla danej wysokości jeśli co najmniej 75% z 20 wyników pomiarów kończyło takim rezultatem. Stężenie detergentu w tym pomiarze wynosiło 20%, a napięcie powierzchniowe to (23.6 ± 0.4) ✕ 10-3 N/m. Jak widać z wyników przedstawionych na (Rys. 6), wraz ze wzrostem średnicy błony mydlanej jej przepuszczalność maleje – tj. potrzebna jest większa energia kulki aby przez nią przejść. Rezultat ten zgadza się z przewidywaniami teoretycznymi.
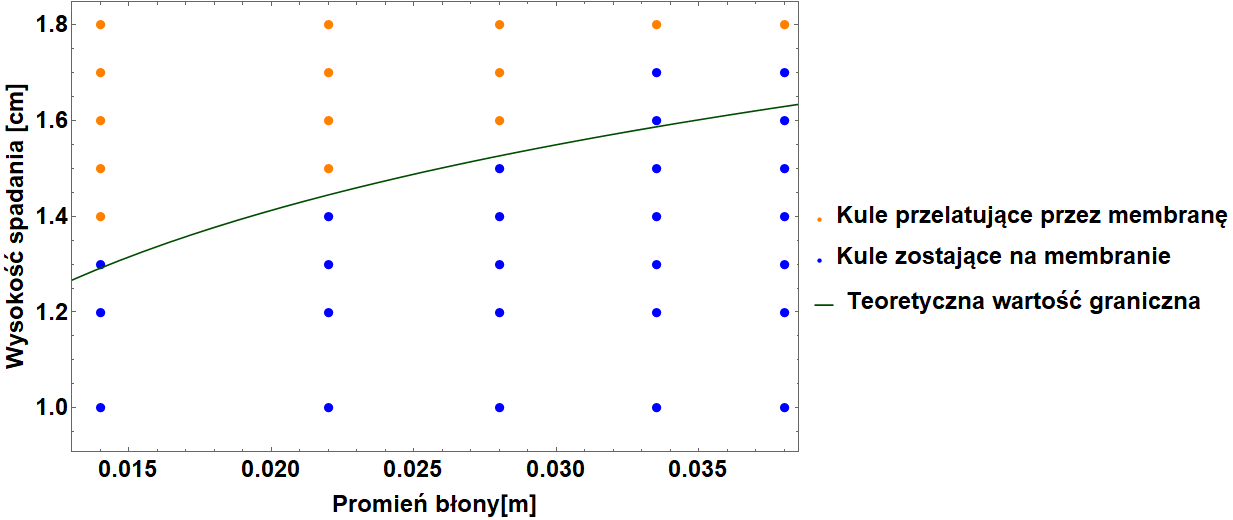
W kolejnej serii pomiarowej zbadano jak promień kulki wpływa na przepuszczalność membrany. W tym celu użyto kulek o promieniach: 0.75 mm, 1.5 mm, 2 mm, 3.5 mm . Kulki różniły się także masą. Użyty w tym pomiarze płyn mydlany miał stężenie detergentu 30% i napięcie powierzchniowe (23.9 ± 0.2) ✕ 10-3 N/m. Okazało się, że tylko kulki o najmniejszej masie zatrzymywały się na błonę. Wyniki pomiarów oraz porównanie z modelem teoretycznym przedstawiono na wykresie.
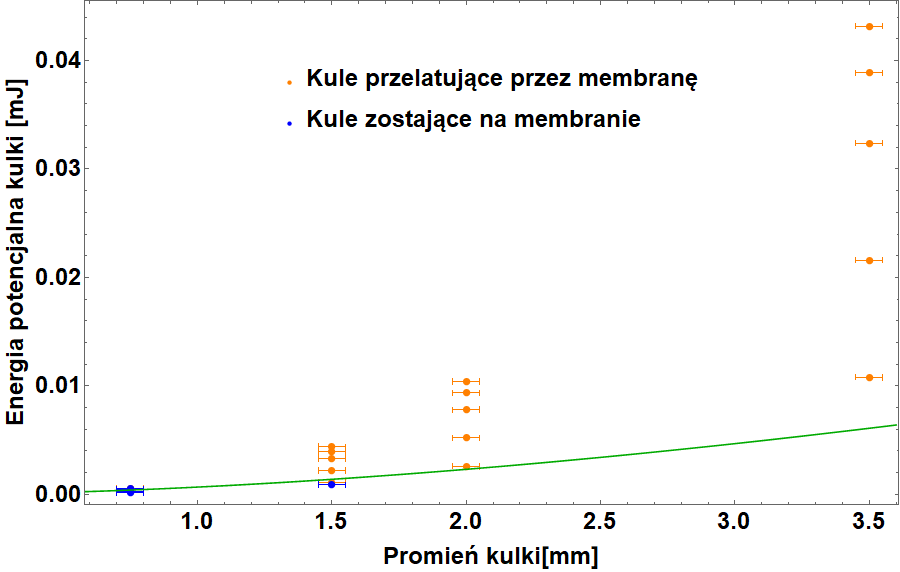
Podsumowanie
Wprowadzony model teoretyczny, oparty o analizę sił działających między błonką a kilką oraz zasadę zachowania energii, wskazaliśmy dwa warunki jakie muszą być spełnione aby spadająca kulka została zatrzymana przez filtr mydlany. Mieszając odpowiednie proporcje detergentu, wody i gliceryny, przygotowaliśmy płyn mydlany, który pozwolił na otrzymanie długotrwałej błony mydlanej. Przepuszczalność membrany została przebadana dla szerokiego zakresu średnic i mas kulek, wysokości upuszczania kulek na błonę mydlaną oraz średnicy błony. Najmniejsze dostępne kulek o promieniu 1 mm potrafiły przelecieć przez błonę nie powodując jej pęknięcia, gdy były zrzucane na nią z maksymalnej wysokości 60cm.
Bibliografia
[1] B. B. Stogin, L. Gockowski, H. Feldstein, H. Claure, J. Wang, and T.-S. Wong, Free-standing liquid membranes as unusual particle separators
Sci. Adv., American Association for the Advancement of Science (AAAS), 2018, 4, eaat3276
[2] A. Le Goff, L. Courbin, H. A. Stone, D. Quéré, Energy absorption in a bamboo foam, EPL (Europhysics Letters), IOP Publishing, 2008, 84, 36001
Podziękowania
Badania były prowadzone przez Klub Naukowy Fenix w ramach projektu Ochota na Naukę.

